8. Analysis of CRYPTEC project cryptographic algorithms¶

CRYPTREC is the Cryptography Research and Evaluation Committees set up by the Japanese Government to evaluate and recommend cryptographic techniques for government and industrial use. It is comparable in many respects to the European Union’s NESSIE project and to the Advanced Encryption Standard process run by NIST in the U.S.. In this chapter, certain cryptographic algorithms from CRYPTEC project candidates are analysed.

Below you can find a legend describing the cryptographic criteria used in this chapter:

NL	Nonlinearity
NL2	2-nd order nonlinearity
LD	Linearity distance
DEG	Algebraic degree
AI	Algebraic immunity
MAXAC	Absolute indicator
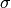$\sigma$	Sum-of-squares indicator
LP	Linear potential
DP	Differential Potential

Hyperlinks to representations

Open the hyperlinks to representations below in a new browser window or in a new tab.

8.1. CIPHERUNICORN-E ¶

8.1.1. Description ¶

CIPHERUNICORN-E is a block cipher created by NEC in 1998. It was among the cryptographic techniques recommended for Japanese government use by CRYPTREC in 2003, however, has been dropped to “candidate” by CRYPTREC revision in 2013. It has four 8x8 S-boxes: S0,S1,S2,S3

8.1.2. Summary ¶

S-box	NL	LD	DEG	AI	MAXAC	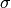$\sigma$	LP	DP
S0	112	56	7	4	32	133120	0.015625	0.015625
S1	112	56	7	4	32	133120	0.015625	0.015625
S2	112	56	7	4	32	133120	0.015625	0.015625
S3	112	56	7	4	32	133120	0.015625	0.015625

8.1.3. S0 ¶

8.1.3.1. Representations ¶

Polynomial function over 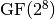$\gf{GF(2^8)}$ with irreducible polynomial 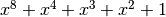$x^8 + x^4 + x^3 + x^2 + 1$ : Trace representation

Polynomial representation in ANF

Truth Table

ANF Table

Characteristic function

Walsh Spectrum

Walsh Spectrum representation (except first row and column):

Linear Profile

Differential Profile

Autocorrelation Spectrum

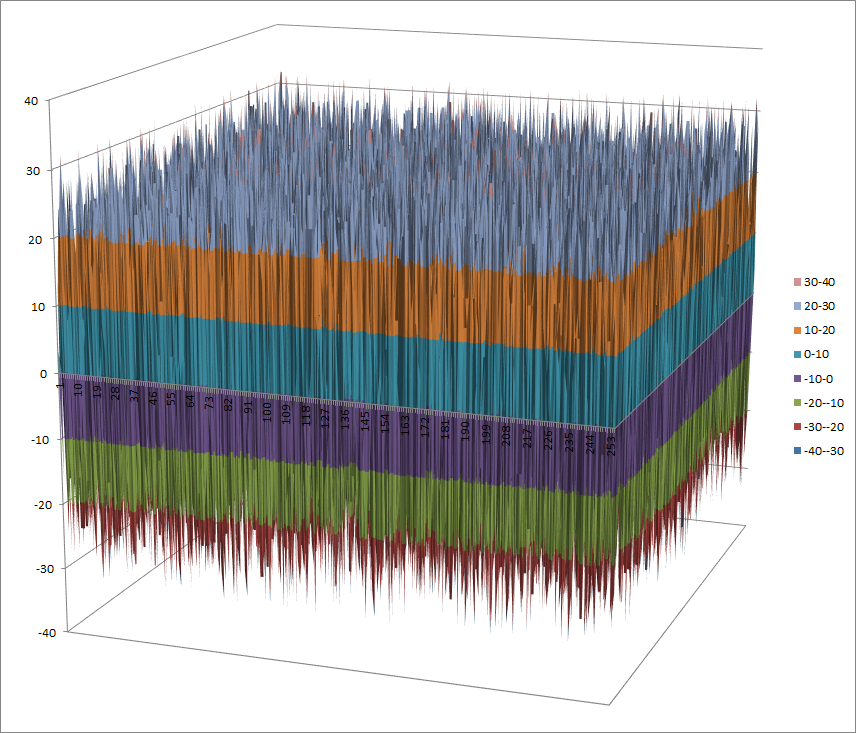
8.1.3.2. Other useful information in cryptanalysis ¶

Cycle structure:

Cycle length	Number of cycles
2	1
45	1
209	1

There are no linear structures

It has no fixed points. It has no negated fixed points.

8.1.4. S1 ¶

8.1.4.1. Representations ¶

Polynomial function over 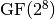$\gf{GF(2^8)}$ with irreducible polynomial 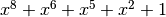$x^8 + x^6 + x^5 + x^2 + 1$ : Trace representation

Polynomial representation in ANF

Truth Table

ANF Table

Characteristic function

Walsh Spectrum

Walsh Spectrum representation (except first row and column):

Linear Profile

Differential Profile

Autocorrelation Spectrum

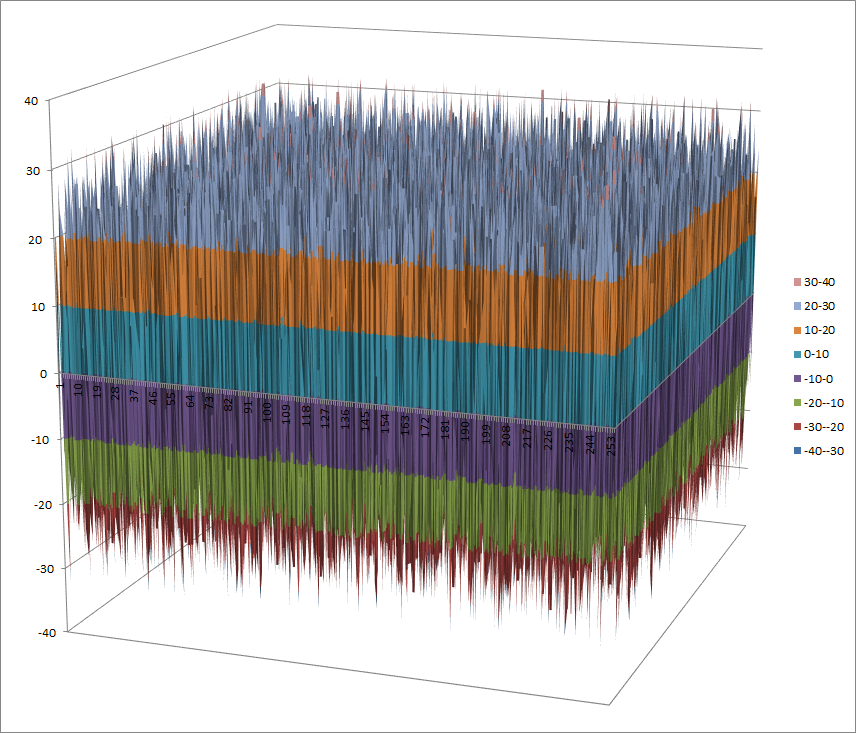
8.1.4.2. Other useful information in cryptanalysis ¶

Cycle structure:

Cycle length	Number of cycles
2	1
49	1
205	1

There are no linear structures

It has no fixed points. It has no negated fixed points.

8.1.5. S2 ¶

8.1.5.1. Representations ¶

Polynomial function over 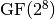$\gf{GF(2^8)}$ with irreducible polynomial 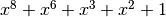$x^8 + x^6 + x^3 + x^2 + 1$ : Trace representation

Polynomial representation in ANF

Truth Table

ANF Table

Characteristic function

Walsh Spectrum

Walsh Spectrum representation (except first row and column):

Linear Profile

Differential Profile

Autocorrelation Spectrum

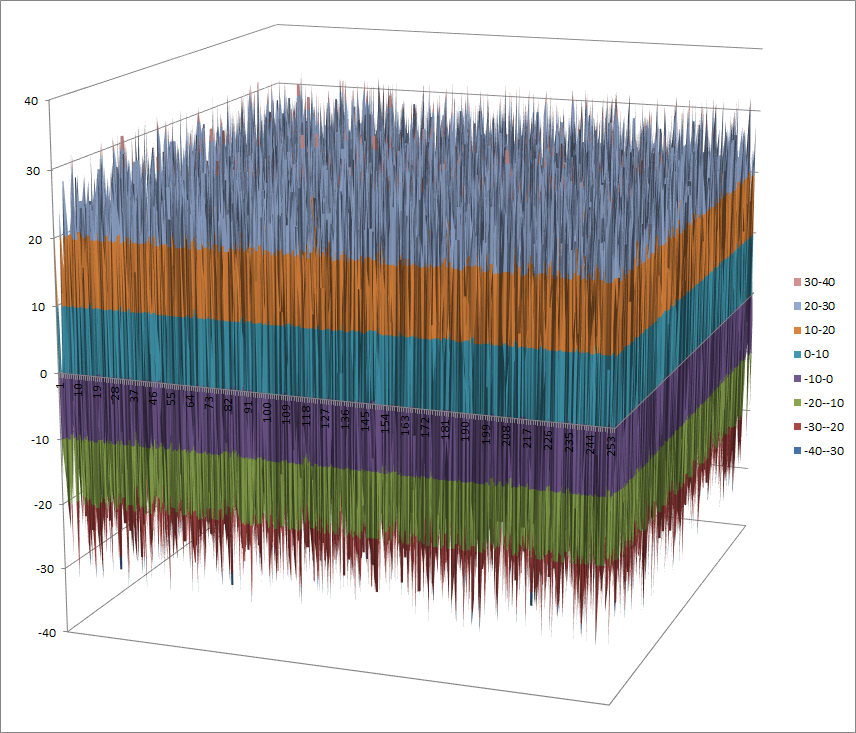
8.1.5.2. Other useful information in cryptanalysis ¶

Cycle structure:

Cycle length	Number of cycles
4	1
6	1
33	1
73	1
140	1

There are no linear structures

It has no fixed points. It has no negated fixed points.

8.1.6. S3 ¶

8.1.6.1. Representations ¶

Polynomial function over 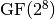$\gf{GF(2^8)}$ with irreducible polynomial 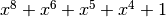$x^8 + x^6 + x^5 + x^4 + 1$ : Trace representation

Polynomial representation in ANF

Truth Table

ANF Table

Characteristic function

Walsh Spectrum

Walsh Spectrum representation (except first row and column):

Linear Profile

Differential Profile

Autocorrelation Spectrum

8.1.6.2. Other useful information in cryptanalysis ¶

Cycle structure:

Cycle length	Number of cycles
3	2
8	1
21	1
221	1

There are no linear structures

It has no fixed points.

It has 2 negated fixed points: (0,0,1,0,0,0,1,1), (0,1,1,1,1,1,1,1)

8.2. CLEFIA ¶

8.2.1. Description ¶

CLEFIA is a proprietary block cipher algorithm, developed by Sony. It is intended to be used in DRM systems. It is among the cryptographic techniques recommended candidate for Japanese government use by CRYPTREC revision in 2013. It has two 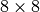$8 \times 8$ S-boxes: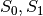 $S_0,S_1$

8.2.2. Summary ¶

S-box	NL	LD	DEG	AI	MAXAC	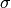$\sigma$	LP	DP
S0	100	40	6	4	96	269056	0.0478515625	0.0390625
S1	112	56	7	4	32	133120	0.015625	0.015625

8.2.3. S0 ¶

8.2.3.1. Representations ¶

Polynomial function over 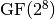$\gf{GF(2^8)}$ with irreducible polynomial 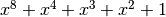$x^8 + x^4 + x^3 + x^2 + 1$ : Trace representation

Polynomial representation in ANF

Truth Table

ANF Table

Characteristic function

Walsh Spectrum

Walsh Spectrum representation (except first row and column):

Linear Profile

Differential Profile

Autocorrelation Spectrum

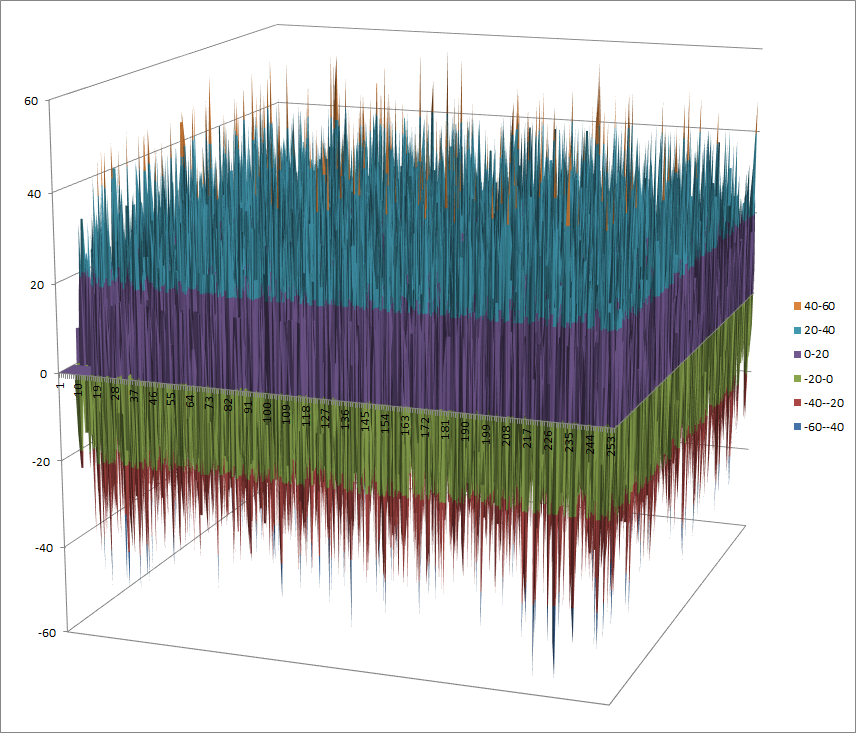
8.2.3.2. Other useful information in cryptanalysis ¶

Cycle structure:

Cycle length	Number of cycles
4	1
5	2
17	1
109	1
116	1

There are no linear structures

It has no fixed points.

It has 2 negated fixed points: (0,1,0,0,0,0,0,1), (1,1,1,1,1,1,0,1)

8.2.3.3. Construction ¶

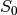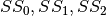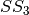$S_0$ is generated by combining four 4-bit S-boxes $SS_0,SS_1,SS_2$ and $SS_3$ in the following way:

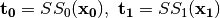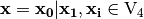
Step 1. $\vec{t_0}=SS_0(\vec{x_0}), \ \vec{t_1}=SS_1(\vec{x_1})$ where $\vec{x} = \vec{x_0} | \vec{x_1}, \vec{x_i} \in \gf{V_4}$

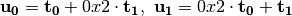
Step 2. $\vec{u_0}=\vec{t_0}+0x2 \cdot \vec{t_1}, \ \vec{u_1}= 0x2 \cdot \vec{t_0}+\vec{t_1}$

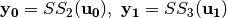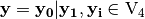
Step 3. $\vec{y_0}=SS_2(\vec{u_0}), \ \vec{y_1}=SS_3(\vec{u_1})$ where $\vec{y} = \vec{y_0} | \vec{y_1}, \vec{y_i} \in \gf{V_4}$

Tables of CLEFIA S-boxes 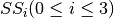$SS_i (0 \leq i \leq 3)$ :

x	0	1	2	3	4	5	6	7	8	9	a	b	c	d	e	f
SS0(x)	e	6	c	a	8	7	2	f	b	1	4	0	5	9	d	3
SS1(x)	6	4	0	d	2	b	a	3	9	c	e	f	8	7	5	1
SS2(x)	b	8	5	e	a	6	4	c	f	7	2	3	1	0	d	9
SS3(x)	a	2	6	d	3	4	5	e	0	7	8	9	b	f	c	1

The multiplication in 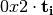$0x2 \cdot \vec{t_i}$ is performed in 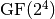$\gf{GF(2^4)}$ defined by the lexicographically first primitive polynomial 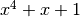$x^4+x+1$ . Here we provide the table of multiplication of 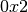$0x2$ with an element modulo 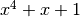$x^4+x+1$ . The entries in the Table are represented in hexadecimal notation for compactness. The column indices represent the element to be multplied by 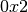$0x2$ modulo 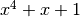$x^4+x+1$ , and the product is the corresponding entry in the column.

Table of the multiplication 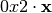$0x2 \cdot \vec{x}$ :

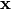$\vec{x}$	0	1	2	3	4	5	6	7	8	9	a	b	c	d	e	f
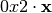$0x2 \cdot \vec{x}$	0	2	4	6	8	a	c	e	3	1	7	5	b	9	f	d

Next figure shows the construction of 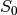$S_0$ :

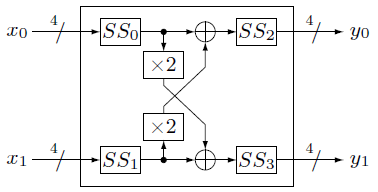
Hence, CLEFIA S0 can be denoted by:

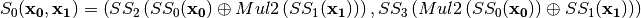
$S_0(\vec{x_0},\vec{x_1}) = \left( SS_2 \left( SS_0(\vec{x_0}) \oplus Mul2 \left( SS_1(\vec{x_1}) \right) \right), SS_3 \left( Mul2 \left( SS_0(\vec{x_0}) \right) \oplus SS_1(\vec{x_1}) \right) \right)$

Note that the symbol $\circ$ refers to the composition of functions, $\oplus$ refers to the direct sum of functions and $Mul2(\vec{x}) = 0x2 \cdot \vec{x}$ .

The criteria of several constructions in 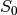$S_0$ are summarized in the following tables:

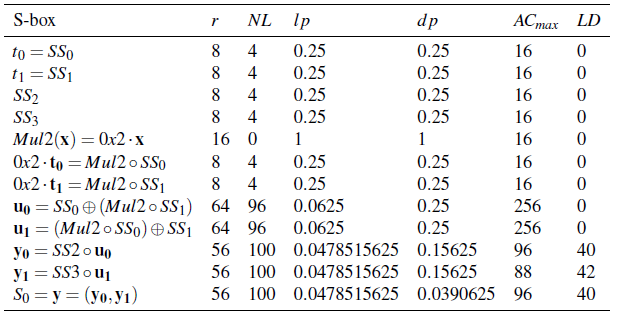
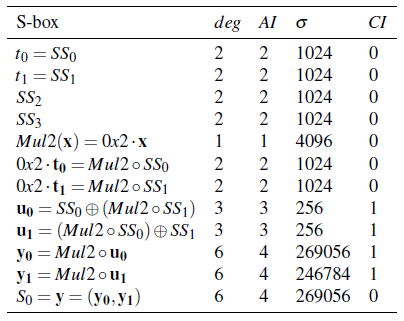
You can find a program which calculates the Truth Tables of these constructions in chapter “Operations and constructions over Vector Boolean Functions”, section “Addition of coordinate functions”.

8.2.3.3.1. Mul2¶

Let 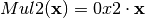$Mul2(\vec{x}) = 0x2 \cdot \vec{x}$ the multiplication in 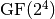$\gf{GF(2^4)}$ defined by the primitive polynomial 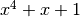$x^4+x+1$ as in CLEFIA cipher.

Polynomial representation in ANF

Truth Table

ANF Table

Characteristic function

Walsh Spectrum

Linear Profile

Differential Profile

Autocorrelation Spectrum

Cycle structure:

Cycle length	Number of cycles
1	1
15	1

There are 225 linear structures

Linear Structures

It has 1 fixed point: (0,0,0,0)

It has 1 negated fixed point: (0,1,0,1)

8.2.3.3.2. 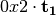$0x2 \cdot \vec{t_1}$ ¶

The operation 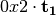$0x2 \cdot \vec{t_1}$ in Step 2 can be interpreted as the composition of 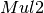$Mul2$ and $SS_1$ .

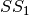Polynomial representation in ANF

Truth Table

ANF Table

Characteristic function

Walsh Spectrum

Linear Profile

Differential Profile

Autocorrelation Spectrum

Cycle structure:

Cycle length	Number of cycles
1	2
2	2
10	1

There are 3 linear structures:

([0 0 1 0],[0 1 0 1])
([0 1 0 0],[0 1 0 1])
([0 1 1 0],[0 1 0 1])

It has 2 fixed points: (0,1,0,0), (0,1,0,1)

It has 1 negated fixed point: (1,1,0,0)

8.2.3.3.3. 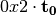$0x2 \cdot \vec{t_0}$ ¶

The operation 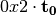$0x2 \cdot \vec{t_0}$ in Step 2 can be interpreted as the composition of 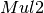$Mul2$ and $SS_0$ .

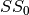Polynomial representation in ANF

Truth Table

ANF Table

Characteristic function

Walsh Spectrum

Linear Profile

Differential Profile

Autocorrelation Spectrum

Cycle structure:

Cycle length	Number of cycles
16	1

There are 3 linear structures:

([0 0 1 1],[1 0 0 1])
([1 0 0 1],[1 0 0 1])
([1 0 1 0],[1 0 0 1])

It has no fixed points.

It has 1 negated fixed point: (0,0,0,0)

8.2.3.3.4. 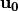$\vec{u_0}$ ¶

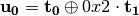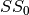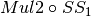The operation $\vec{u_0} = \vec{t_0} \oplus 0x2 \cdot \vec{t_1}$ in Step 2 can be interpreted as the direct sum of $SS_0$ and $Mul2 \circ SS_1$ .

Polynomial representation in ANF

Truth Table

ANF Table

Characteristic function

Walsh Spectrum

Linear Profile

Differential Profile

Autocorrelation Spectrum

There are 6 linear structures:

([0 0 0 0 0 0 1 0],[0 1 0 1])
([0 0 0 0 0 1 0 0],[0 1 0 1])
([0 0 0 0 0 1 1 0],[0 1 0 1])
([0 0 1 1 0 0 0 0],[1 1 0 0])
([1 0 0 1 0 0 0 0],[1 1 0 0])
([1 0 1 0 0 0 0 0],[1 1 0 0])

8.2.3.3.5. 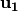$\vec{u_1}$ ¶

The operation 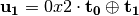$\vec{u_1}= 0x2 \cdot \vec{t_0} \oplus \vec{t_1}$ in Step 2 can be interpreted as the direct sum of 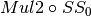$Mul2 \circ SS_0$ and $SS_1$ .

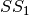Polynomial representation in ANF

Truth Table

ANF Table

Characteristic function

Walsh Spectrum

Linear Profile

Differential Profile

Autocorrelation Spectrum

There are 6 linear structures:

([0 0 0 0 0 0 1 0],[1 0 1 0])
([0 0 0 0 0 1 0 0],[1 0 1 0])
([0 0 0 0 0 1 1 0],[1 0 1 0])
([0 0 1 1 0 0 0 0],[1 0 0 1])
([1 0 0 1 0 0 0 0],[1 0 0 1])
([1 0 1 0 0 0 0 0],[1 0 0 1])

8.2.3.3.6. 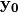$\vec{y_0}$ ¶

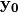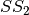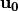In the Step 3, $\vec{y_0}$ is obtained by composing $SS_2$ S-box with $\vec{u_0}$ .

Polynomial representation in ANF

Truth Table

ANF Table

Characteristic function

Walsh Spectrum

Linear Profile

Differential Profile

Autocorrelation Spectrum

There are no linear structures.

8.2.3.3.7. 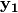$\vec{y_1}$ ¶

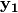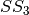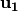In the Step 3, $\vec{y_1}$ is obtained by composing $SS_3$ S-box with $\vec{u_1}$ .

Polynomial representation in ANF

Truth Table

ANF Table

Characteristic function

Walsh Spectrum

Linear Profile

Differential Profile

Autocorrelation Spectrum

There are no linear structures.

8.2.4. S1 ¶

8.2.4.1. Representations ¶

Polynomial function over 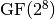$\gf{GF(2^8)}$ with irreducible polynomial 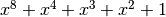$x^8 + x^4 + x^3 + x^2 + 1$ : Trace representation

Polynomial representation in ANF

Truth Table

ANF Table

Characteristic function

Walsh Spectrum

Walsh Spectrum representation (except first row and column):

Linear Profile

Differential Profile

Autocorrelation Spectrum

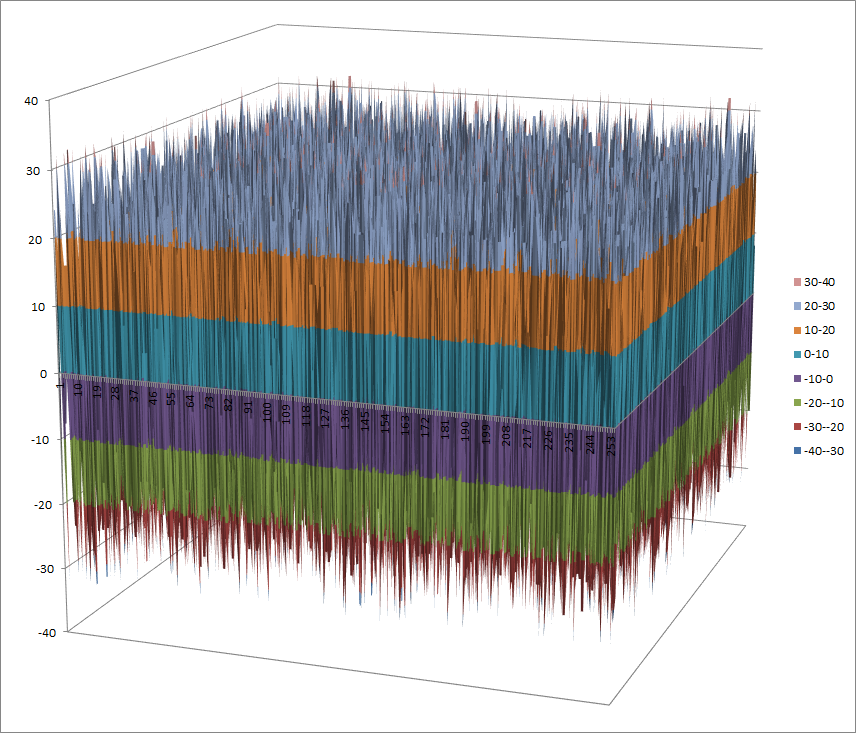
8.2.4.2. Other useful information in cryptanalysis ¶

Cycle structure:

Cycle length	Number of cycles
256	1

There are no linear structures

It has no fixed points.

It has 1 negated fixed point: (0,0,1,1,1,0,1,0)

8.3. Hierocrypt3 ¶

8.3.1. Description ¶

Hierocrypt3 and Hierocrypt-L1 are block ciphers created by Toshiba in 2000. They were submitted to the NESSIE project, but were not selected. Both algorithms were among the cryptographic techniques recommended for Japanese government use by CRYPTREC in 2003, however, both have been dropped to “candidate” by CRYPTREC revision in 2013. Both of them have the same 8x8 S-box: S

8.3.2. Summary ¶

S-box	NL	LD	DEG	AI	MAXAC	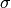$\sigma$	LP	DP
S	112	56v	7	4	32	133120	0.015625	0.015625

8.3.3. S ¶

8.3.3.1. Representations ¶

Polynomial function over 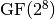$\gf{GF(2^8)}$ with irreducible polynomial 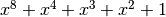$x^8 + x^4 + x^3 + x^2 + 1$ : Trace representation

Polynomial representation in ANF

Truth Table

ANF Table

Characteristic function

Walsh Spectrum

Walsh Spectrum representation (except first row and column):

Linear Profile

Differential Profile

Autocorrelation Spectrum

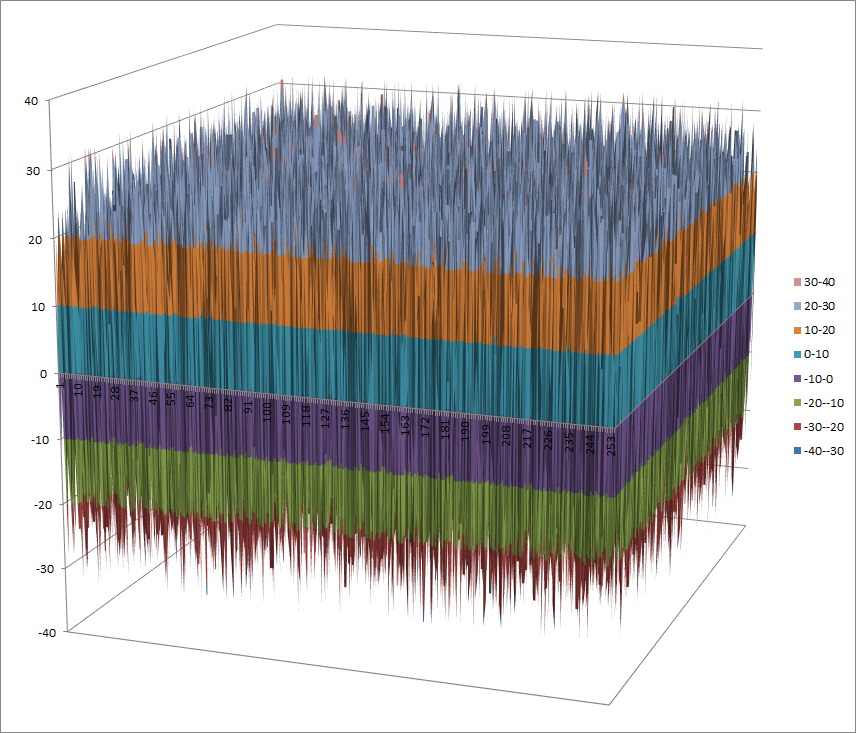
8.3.3.2. Other useful information in cryptanalysis ¶

Cycle structure:

Cycle length	Number of cycles
1	1
2	1
3	1
109	1
141	1

There are no linear structures

It has 1 fixed point: (0,1,1,0,0,1,1,1)

It has 2 negated fixed points: (0,0,0,1,0,1,1,1), (1,0,0,1,0,1,0,0)

8.4. SC2000 ¶

8.4.1. Description ¶

SC2000 is a block cipher invented by a research group at Fujitsu Labs. It was submitted to the NESSIE project, but was not selected. It was among the cryptographic techniques recommended for Japanese government use by CRYPTREC in 2003, however, has been dropped to “candidate” by CRYPTREC revision in 2013. It has three 3 S-boxes: S4,S5,S6

8.4.2. Summary ¶

S-box	size	NL	NL2	LD	DEG	AI	MAXAC	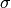$\sigma$	LP	DP
S4	4x4	4	0	0	2	2	16	1024	0.25	0.25
S5	5x5	12	6	6	3	3	8	2048	0.0625	0.0625
S6	6x6	24	14	12	5	3	16	8704	0.0625	0.0625

8.4.3. S4 ¶

8.4.3.1. Representations ¶

Polynomial representation in ANF

Truth Table

ANF Table

Characteristic function

Walsh Spectrum

Walsh Spectrum representation (except first row and column):

Linear Profile

Differential Profile

Autocorrelation Spectrum

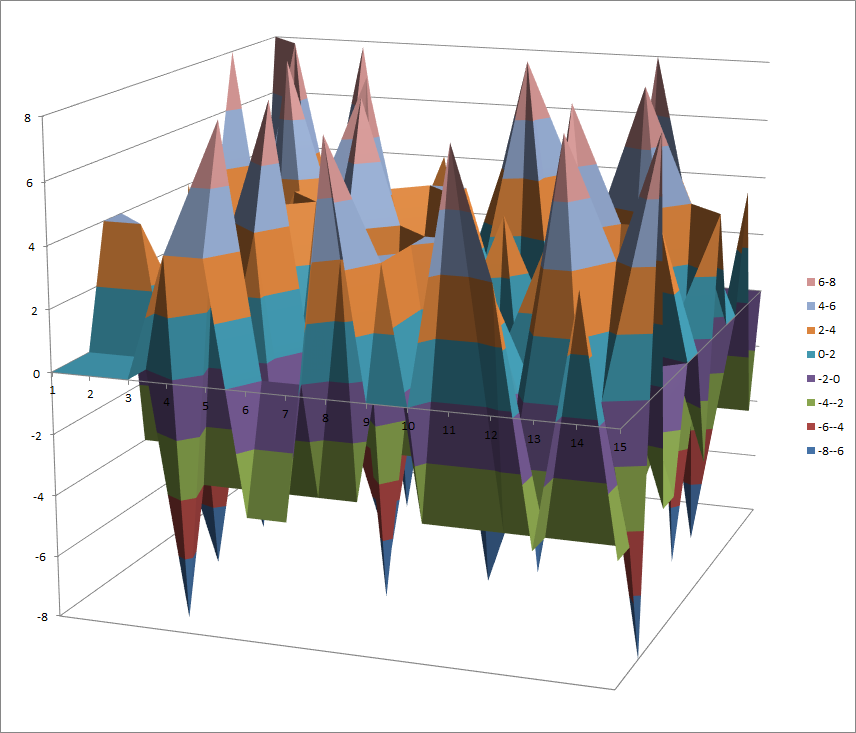
8.4.3.2. Other useful information in cryptanalysis ¶

Cycle structure:

Cycle length	Number of cycles
2	1
3	1
11	1

There are 3 linear structures:

([0 1 0 1],[0 0 1 1])
([1 0 0 1],[0 0 1 1])
([1 1 0 0],[0 0 1 1])

It has no fixed points.

It has 2 negated fixed points: (0,0,1,1), (1,0,0,1)

8.4.4. S5 ¶

8.4.4.1. Representations ¶

Polynomial representation in ANF

Truth Table

ANF Table

Characteristic function

Walsh Spectrum

Walsh Spectrum representation (except first row and column):

Linear Profile

Differential Profile

Autocorrelation Spectrum

8.4.4.2. Other useful information in cryptanalysis ¶

Cycle structure:

Cycle length	Number of cycles
6	1
8	2
10	1

There are no linear structures

It has no fixed points. It has no negated fixed points

8.4.5. S6 ¶

8.4.5.1. Representations ¶

Polynomial representation in ANF

Truth Table

ANF Table

Characteristic function

Walsh Spectrum

Walsh Spectrum representation (except first row and column):

Linear Profile

Differential Profile

Autocorrelation Spectrum

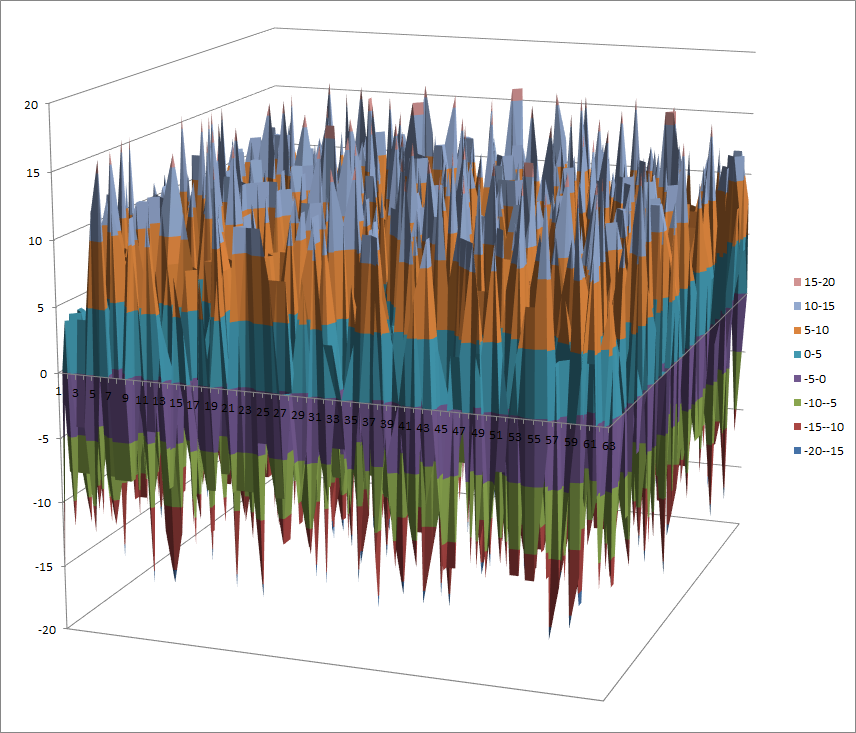
8.4.5.2. Other useful information in cryptanalysis ¶

Cycle structure:

Cycle length	Number of cycles
2	2
9	1
17	1
34	1

There are no linear structures

It has no fixed points. It has no negated fixed points

8. Analysis of CRYPTEC project cryptographic algorithms¶

8.2.3.3.1. Mul2¶

8.2.3.3.2. ¶

8.2.3.3.3. ¶

8.2.3.3.4. ¶

8.2.3.3.5. ¶

8.2.3.3.6. ¶

8.2.3.3.7. ¶

8.2.3.3.2. $0x2 \cdot \vec{t_1}$ ¶

8.2.3.3.3. $0x2 \cdot \vec{t_0}$ ¶

8.2.3.3.4. $\vec{u_0}$ ¶

8.2.3.3.5. $\vec{u_1}$ ¶

8.2.3.3.6. $\vec{y_0}$ ¶

8.2.3.3.7. $\vec{y_1}$ ¶