10. Analysis of other cryptographic algorithms

There are some block ciphers that are relevant either because its wide use or because of its importance in the development of cryptanalysis techniques. In this chapter, some cryptographic algorithms from other block ciphers are analysed.

Below you can find a legend describing the cryptographic criteria used in this chapter:

NL Nonlinearity
NL2 2-nd order nonlinearity
LD Linearity distance
DEG Algebraic degree
AI Algebraic immunity
MAXAC Absolute indicator
\sigma Sum-of-squares indicator
LP Linear potential
DP Differential Potential

Hyperlinks to representations

Open the hyperlinks to representations below in a new browser window or in a new tab.

10.1. DES

10.1.1. Description

DES is a block cipher used for securing sensitive but unclassified material by U.S. Government agencies and became the de facto encryption standard for commercial transactions in the private sector up to December 6, 2001. It was superseded by AES. DES has eight 6x4 S-boxes: S1, S2, S3, S4, S5, S6, S7, S8.

10.1.2. Summary

S-box NL NL2 LD DEG AI MAXAC \sigma LP DP
S1 14 8 4 4 2 48 36736 0.31640625 0.25
S2 16 10 2 4 3 56 25984 0.25 0.25
S3 16 10 4 4 3 48 24064 0.25 0.25
S4 16 8 0 3 2 64 40960 0.25 0.25
S5 12 10 6 4 2 40 47104 0.390625 0.25
S6 18 10 4 5 3 48 19456 0.19140625 0.25
S7 14 10 4 5 3 48 34048 0.31640625 0.25
S8 16 10 4 4 3 48 24064 0.25 0.25

10.1.3. S1

10.1.3.2. Other useful information in cryptanalysis

There are no linear structures

10.1.4. S2

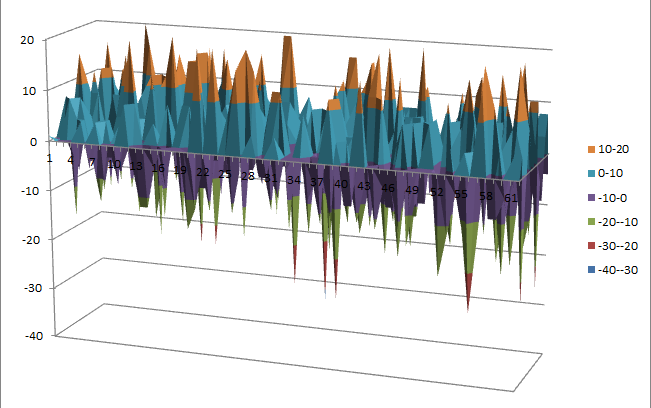
10.1.4.2. Other useful information in cryptanalysis

There are no linear structures

10.1.5. S3

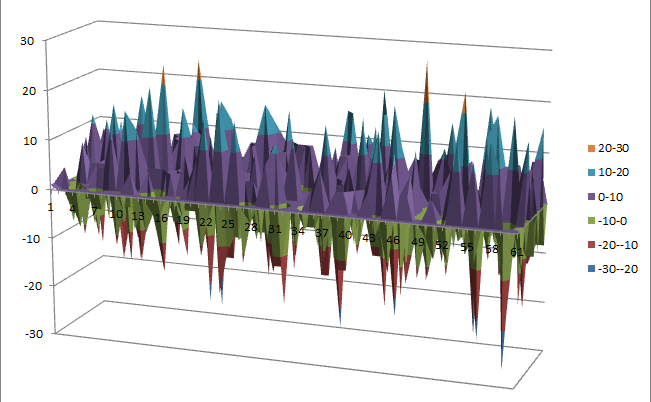
10.1.5.2. Other useful information in cryptanalysis

There are no linear structures

10.1.6. S4

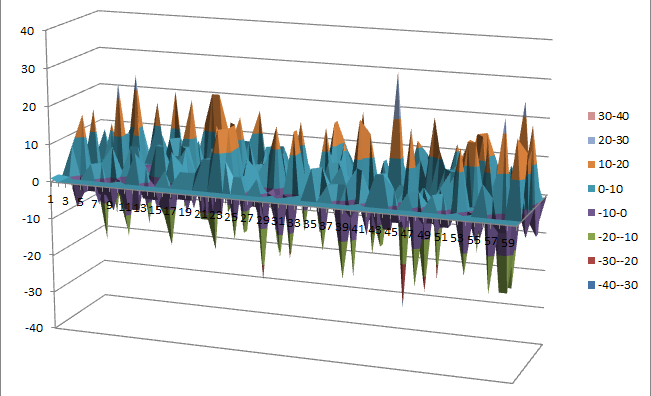
10.1.6.2. Other useful information in cryptanalysis

There are 9 linear structures:

([0 0 0 0 0 1],[0 0 1 1])
([0 0 0 0 0 1],[1 1 0 0])
([0 0 0 0 0 1],[1 1 1 1])
([1 0 1 1 1 0],[0 1 0 1])
([1 0 1 1 1 0],[1 0 1 0])
([1 0 1 1 1 0],[1 1 1 1])
([1 0 1 1 1 1],[0 1 1 0])
([1 0 1 1 1 1],[1 0 0 1])
([1 0 1 1 1 1],[1 1 1 1])

10.1.7. S5

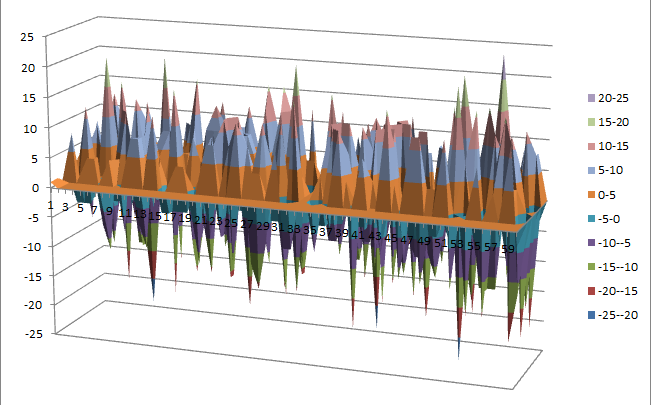
10.1.7.2. Other useful information in cryptanalysis

There are no linear structures

10.1.8. S6

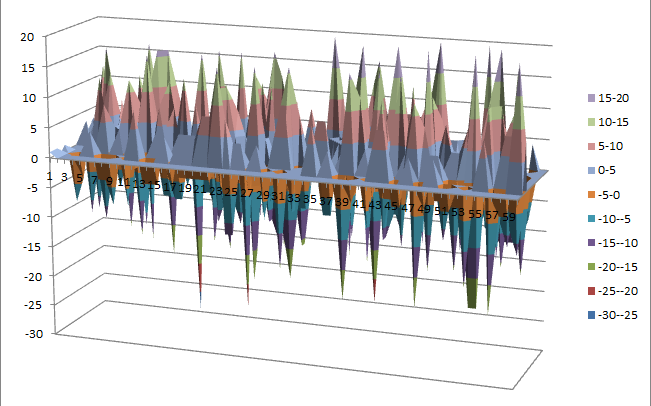
10.1.8.2. Other useful information in cryptanalysis

There are no linear structures

10.1.9. S7

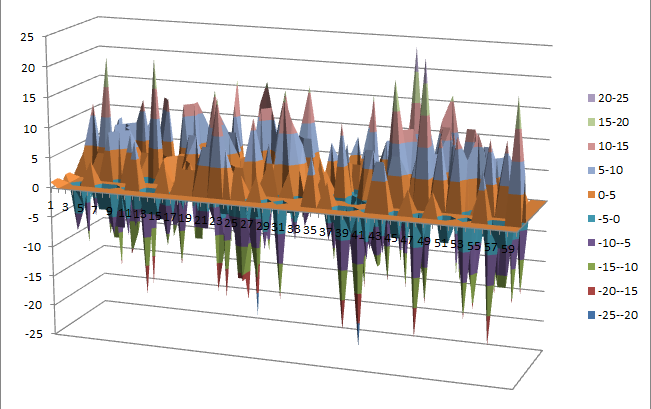
10.1.9.2. Other useful information in cryptanalysis

There are no linear structures

10.1.10. S8

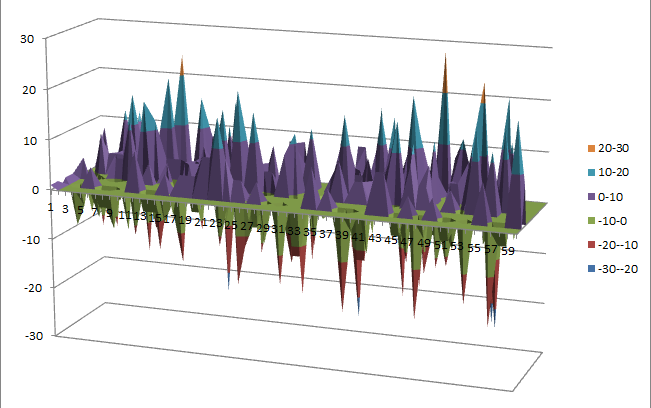
10.1.10.2. Other useful information in cryptanalysis

There are no linear structures

10.2. KASUMI

10.2.1. Description

KASUMI is a block cipher used in UMTS, GSM, and GPRS mobile communications systems. UMTS uses KASUMI in the confidentiality (f8) and integrity algorithms (f9) named UEA1 and UIA1, respectively. GSM employs KASUMI in the A5/3 key stream generator whereas GPRS does so in the GEA3 key stream generator. This cipher has two S-boxes: a 7x7 S-box called S7 and a 9x9 S-box called S9.

10.2.2. Summary

S-box size NL NL2 LD DEG AI MAXAC \sigma LP DP
S7 7x7 56 36 28 3 3 16 32768 0.015625 0.015625
S9 9x9 240 0 0 2 2 512 524288 0.00390625 0.00390625

10.2.3. S7

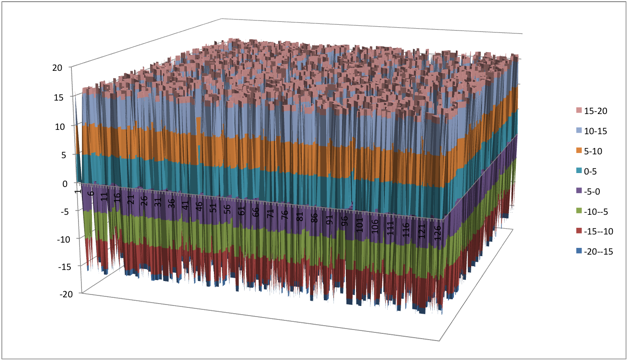
10.2.3.2. Other useful information in cryptanalysis

Cycle structure:

Cycle length Number of cycles
1 1
13 1
22 1
92 1

There are no linear structures

It has 1 fixed point: (0,0,1,1,0,1,1)

It has no negated fixed points

10.2.4. S9

10.2.4.2. Other useful information in cryptanalysis

Cycle structure:

Cycle length Number of cycles
1 2
2 1
12 1
26 1
74 1
121 1
275 1

There are 511 linear structures:

Linear structures

It has 1 fixed point: (0,1,0,0,1,0,1,1,1)

It has 1 negated fixed points (1,0,0,0,1,1,0,0,0)

10.2.5. FI

Algebraic degree from key 00000 to 65535

Cycle structure from key 00000 to 65535

Fixed and negated points from key 00000 to 65535

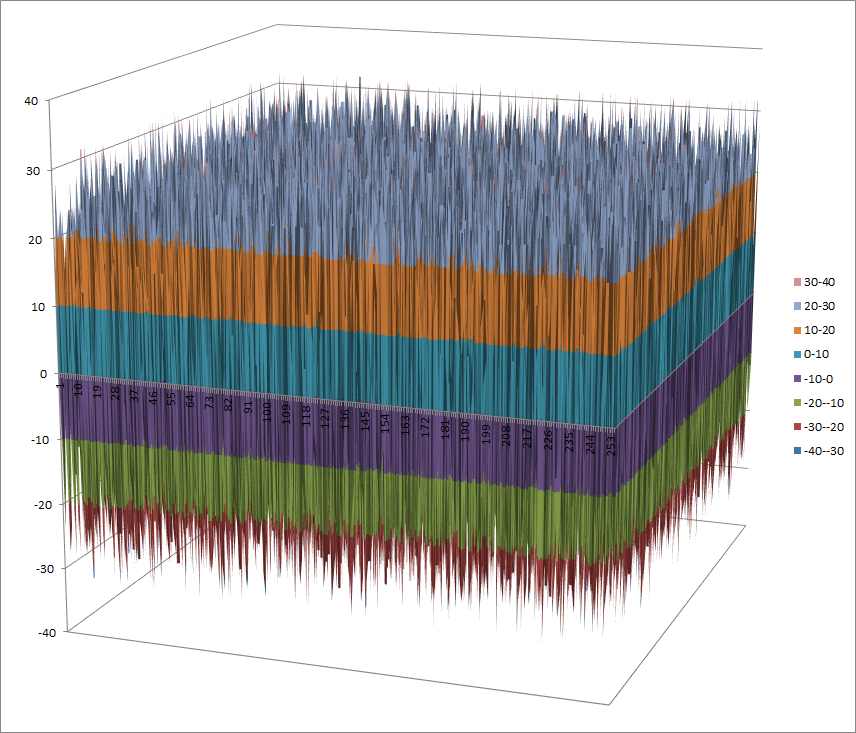
Nonlinearities from key 00000 to 65535

Graphical display of the distribution of the nonlinearities of FI:

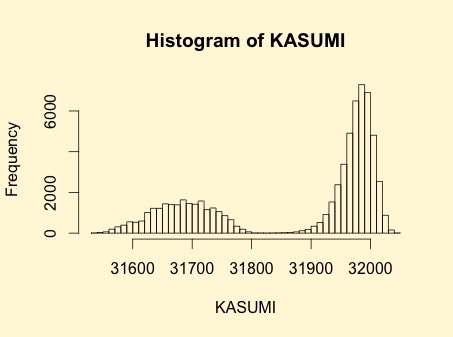
images/hist-KASUMI.jpeg
Descriptive Statistics of FI nonlinearities
Unique Values 478
Min 31534
Max 32049
Mean 31878.7986
Mean Deviation 132.083019
1st Quartile 31720
Median 31963
3rd Quartile 31989
Mode 31995
Range 515
Variance 20879.009
Standard Deviation 144.4957
Kkewness -0.7622
Kurtosis -1.1463
P0.5 31572
P1 31582
P5 31627
P95 32011
P99 32023
P99.5 32027

10.3. MacGuffin

10.3.1. Description

MacGuffin is a block cipher uses a F-function which consists of the 8 S-boxes of the DES, but the two middle output bits of each S-box are neglected in order to obtain a 16-bit output. MacGuffin has eight 6x2 S-boxes: S1, S2, S3, S4, S5, S6, S7, S8.

10.3.2. Summary

S-box NL NL2 LD DEG AI MAXAC \sigma LP DP
S1 18 12 8 5 3 32 20224 0.19140625 0.53125
S2 18 10 6 5 3 40 19840 0.19140625 0.5625
S3 18 10 4 5 3 48 21376 0.19140625 0.53125
S4 16 8 0 4 2 64 25600 0.25 0.5
S5 20 12 8 5 3 32 16000 0.140625 0.5
S6 20 10 4 5 3 48 19456 0.140625 0.4375
S7 18 10 4 5 3 48 23296 0.19140625 0.53125
S8 20 10 6 5 3 40 14848 0.140625 0.5

10.3.3. S1

10.3.3.2. Other useful information in cryptanalysis

There are no linear structures

10.3.4. S2

10.3.4.2. Other useful information in cryptanalysis

There are no linear structures

10.3.5. S3

10.3.5.2. Other useful information in cryptanalysis

There are no linear structures

10.3.6. S4

10.3.6.2. Other useful information in cryptanalysis

There are 1 linear structure:

([1 0 1 1 1 1],[1 1])

10.3.7. S5

10.3.7.2. Other useful information in cryptanalysis

There are no linear structures

10.3.8. S6

10.3.8.2. Other useful information in cryptanalysis

There are no linear structures

10.3.9. S7

10.3.9.2. Other useful information in cryptanalysis

There are no linear structures

10.3.10. S8

10.3.10.2. Other useful information in cryptanalysis

There are no linear structures

10.4. Mini-AES

10.4.1. Description

Raphael Chung-Wei Phan presented a version of the AES [Phan02miniadvanced], with all the parameters significantly reduced while preserving its original structure. This Mini version is purely educational and is designed to grasp the underlying concepts of Rijndael-like ciphers. It may also serve as a testbed for starting cryptanalysts to experiment with various cryptanalytic attacks. The Mini-AES cipher is a 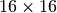16 \times 16 vector Boolean function and the Mini-AES encryption is performed with a secret key of 16 bits.

The Mini-AES S-box is called NibbleSub, and defines a simple operation that substitutes each input with an output according to a 4x4 substitution table (S-box) given in the table below. These values are, in fact, taken from the first row of the first S-box in DES.

NibbleSub Truth Table
Input Output
0000 1110
0001 0100
0010 1101
0011 0001
0100 0010
0101 1111
0110 1011
0111 1000
1000 0011
1001 1010
1010 0110
1011 1100
1100 0101
1101 1001
1110 0000
1111 0111

The inverse of the previous table is easily computed by interchanging the input nibble with the output nibble, and then resorting it based on the new input nibble, as given in the table below.

NibbleSubInv Truth Table
Input Output
0000 1110
0001 0011
0010 0100
0011 1000
0100 0001
0101 1100
0110 1010
0111 1111
1000 0111
1001 1101
1010 1001
1011 0110
1100 1011
1101 0010
1110 0000
1111 0101

10.4.2. Summary

S-box size NL NL2 LD DEG AI MAXAC 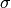\sigma LP DP
NibbleSub 4x4 2 0 0 2 2 16 1408 0.5625 0.5
NibbleSubInv 4x4 2 0 0 2 2 16 11408 0.5625 0.5
MixColumn 8x8 0
0 1 1 256 16777216 1 1

10.4.3. NibbleSub

10.4.3.1. Representations

Polynomial representation in ANF

Truth Table

ANF Table

Characteristic Function

Walsh Spectrum

16 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 -4 -4 0 0 -4 12 4 4 0 0 4 4 0 0
0 0 -4 -4 0 0 -4 -4 0 0 4 4 0 0 -12 4
0 0 0 0 0 0 0 0 4 -12 -4 -4 4 4 -4 -4
0 4 0 -4 -4 -8 -4 0 0 -4 0 4 4 -8 4 0
0 -4 -4 0 -4 0 8 4 -4 0 -8 4 0 -4 -4 0
0 4 -4 8 4 0 0 4 0 -4 4 8 -4 0 0 -4
0 -4 0 4 4 -8 4 0 -4 0 4 0 8 4 0 4
0 0 0 0 0 0 0 0 -4 4 4 -4 4 -4 -4 -12
0 0 -4 -4 0 0 -4 -4 -8 0 -4 4 0 8 4 -4
0 8 -4 4 -8 0 4 -4 4 4 0 0 4 4 0 0
0 8 0 -8 8 0 8 0 0 0 0 0 0 0 0 0
0 -4 8 -4 -4 0 4 0 4 0 4 8 0 4 0 -4
0 4 4 0 -4 8 0 4 -8 -4 4 0 4 0 0 4
0 4 4 0 -4 -8 0 4 -4 0 0 -4 -8 4 -4 0
0 -4 -8 -4 -4 0 4 0 0 -4 8 -4 -4 0 4 0

Walsh Spectrum representation (except first row and column):

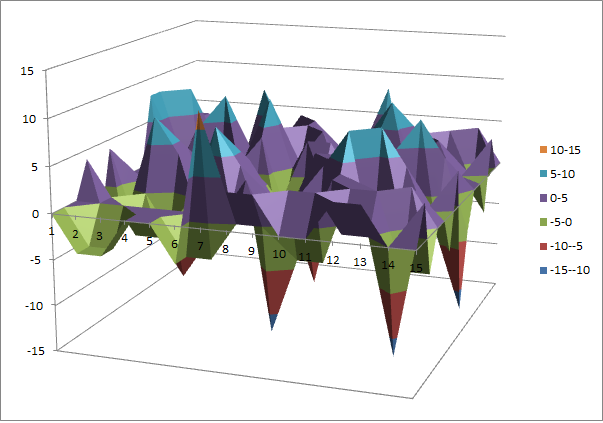
images/Nibble.png

Linear Profile

Differential Profile

Autocorrelation Spectrum

10.4.3.2. Other useful information in cryptanalysis

Cycle structure:

Cycle length Number of cycles
2 1
14 1

There are 7 linear structures:

([0 0 1 1],[0 1 1 1])
([0 1 0 0],[0 1 0 1])
([1 0 1 0],[1 1 1 1])
([1 0 1 1],[0 1 0 1])
([1 1 0 1],[1 0 0 1])
([1 1 1 0],[1 1 1 0])
([1 1 1 1],[0 1 0 1])

It has no fixed points and 2 negated fixed points: (0,0,1,0), (0,1,1,1)

10.4.4. NibbleSubInv

10.4.4.1. Representations

Polynomial representation in ANF

Truth Table

ANF Table

Characteristic Function

Walsh Spectrum

16 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 4 -4 4 -4 0 0 8 8 -4 4 4 -4
0 -4 -4 0 0 -4 -4 0 0 -4 -4 0 8 4 4 -8
0 -4 -4 0 -4 0 8 4 0 -4 4 -8 -4 0 0 -4
0 0 0 0 -4 -4 4 4 0 0 -8 8 -4 -4 -4 -4
0 0 0 0 -8 0 0 -8 0 0 0 0 0 8 -8 0
0 -4 -4 0 -4 8 0 4 0 -4 4 8 4 0 0 4
0 12 -4 0 0 4 4 0 0 -4 -4 0 0 4 4 0
0 4 0 4 0 -4 0 -4 -4 -8 4 0 4 -8 -4 0
0 4 0 -12 -4 0 -4 0 4 0 4 0 0 -4 0 -4
0 0 4 -4 0 -8 4 4 4 -4 0 0 4 4 0 8
0 0 4 -4 4 4 8 0 -4 4 0 0 8 0 -4 -4
0 4 0 4 4 0 -4 8 4 0 4 0 0 4 -8 -4
0 4 0 4 -8 -4 0 4 -4 8 4 0 4 0 4 0
0 0 -12 -4 4 -4 0 0 -4 4 0 0 0 0 -4 4
0 0 4 -4 0 0 -4 4 -12 -4 0 0 -4 |4 |0 0

Walsh Spectrum representation (except first row and column):

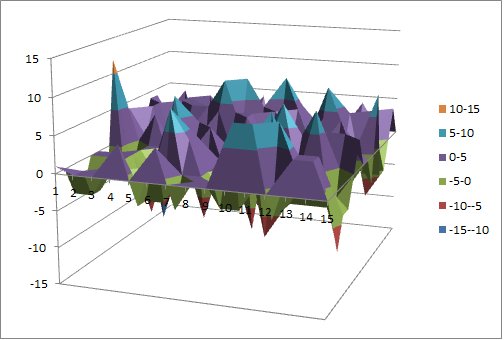
images/NibbleSubInv.png

Linear Profile

Differential Profile

Autocorrelation Spectrum

10.4.4.2. Other useful information in cryptanalysis

Cycle structure:

Cycle length Number of cycles
2 1
14 1

There are 7 linear structures:

([0 0 1 0],[0 0 1 0])
([0 1 0 1],[1 0 1 1])
([1 0 0 0],[0 0 1 1])
([1 0 0 0],[1 0 0 0])
([1 0 0 0],[1 0 1 1])
([1 0 1 0],[0 0 0 1])
([1 1 0 1],[1 0 1 1])

It has no fixed points and 2 negated fixed points: (1,0,0,0), (1,1,0,1)

10.4.5. MixColumn

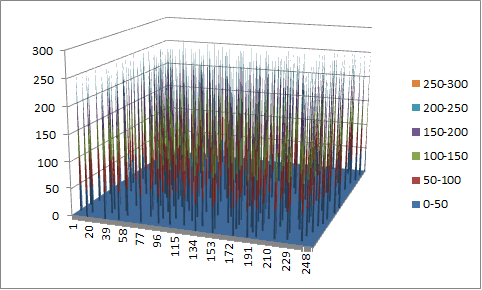
10.4.5.2. Other useful information in cryptanalysis

Cycle structure:

Cycle length Number of cycles
1 16
2 120

There 65025 linear structures

It has 15 fixed points: (0,0,0,0,0,0,0,0), (0,0,0,1,0,0,0,1), (0,0,1,0,0,0,1,0), (0,0,1,1,0,0,1,1), (0,1,0,0,0,1,0,0), (0,1,0,1,0,1,0,1), (0,1,1,0,0,1,1,0), (0,1,1,1,0,1,1,1), (1,0,0,0,1,0,0,0), (1,0,0,1,1,0,0,1), (1,0,1,0,1,0,1,0), (1,0,1,1,1,0,1,1), (1,1,0,0,1,1,0,0), (1,1,0,1,1,1,0,1), (1,1,1,0,1,1,1,0)

It has 16 negated fixed points: (0,0,0,0,1,1,1,0), (0,0,0,1,1,1,1,1), (0,0,1,0,1,1,0,0), (0,0,1,1,1,1,0,1), (0,1,0,0,1,0,1,0), (0,1,0,1,1,0,1,1), (0,1,1,0,1,0,0,0), (0,1,1,1,1,0,0,1), (1,0,0,0,0,1,1,0), (1,0,0,1,0,1,1,1), (1,0,1,0,0,1,0,0), (1,0,1,1,0,1,0,1), (1,1,0,0,0,0,1,0), (1,1,0,1,0,0,1,1), (1,1,1,0,0,0,0,0), (1,1,1,1,0,0,0,1)

10.4.6. ks0

10.4.6.2. Other useful information in cryptanalysis

Cycle structure:

Cycle length Number of cycles
1 65536

10.4.7. ks1

10.4.7.2. Other useful information in cryptanalysis

Cycle structure:

Cycle length Number of cycles
1 1
5 2
10 2
28 1
60 1
1223 1
26097 1
38097 1

10.4.8. ks2

10.4.8.2. Other useful information in cryptanalysis

Cycle structure:

Cycle length Number of cycles
1 1
12 1
15 3
30 1
109 1
385 1
831 1
2472 1
3617 1
9775 1
16777 1
31482 1

10.4.9. mini-AES

Algebraic degree from key 00000 to 65535 is equal to 14

Cycle structure from key 00000 to 65535

Fixed and negated points from key 00000 to 65535

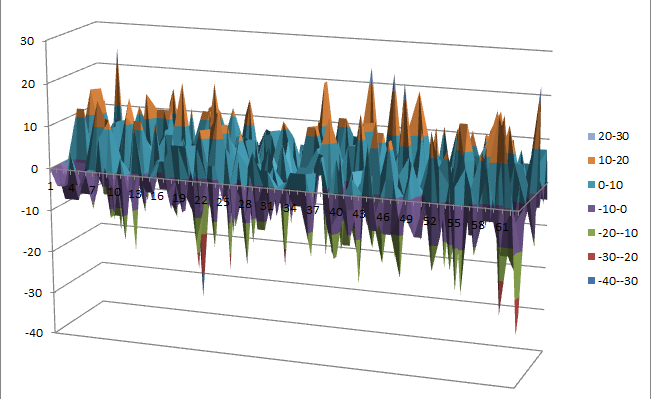
Nonlinearities from key 00000 to 65535

Nonlinearities in ascendent order

Graphical display of the distribution of the nonlinearities of mini-AES:

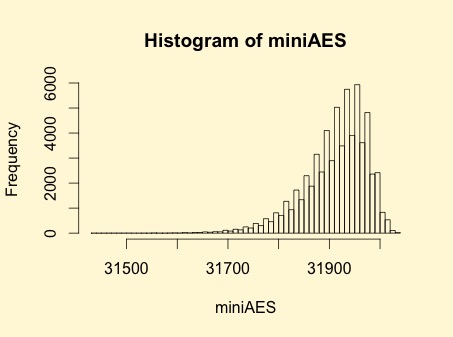
images/hist-miniAES.jpeg
Descriptive Statistics of mini-AES nonlinearities
Unique Values 130
Min 31432
Max 32040
Mean 31912.9894
Mean Deviation 8.6571
1st Quartile 31880
Median 31924
3rd Quartile 31960
Mode 31952
Range 608
Variance 3903.8642
Standard Deviation 62.4809
Kkewness -1.092059
Kurtosis 1.79284
P0.5 31692
P1 31720
P5 31796
P95 31992
P99 32012
P99.5 32016

10.5. Square

10.5.1. Description

Square is a block cipher invented by Joan Daemen and Vincent Rijmen. The design, published in 1997, is a forerunner to Rijndael, which has been adopted as the Advanced Encryption Standard. It has a 8x8 S-box called S.

10.5.2. Summary

S-box size NL LD DEG AI MAXAC \sigma LP DP
S 8x8 112 56 7 4 32 133120 0.015625 0.015625

10.5.3. S

10.5.3.2. Other useful information in cryptanalysis

Cycle structure:

Cycle length Number of cycles
1 2
6 1
8 1
20 1
23 1
197 1

There are no linear structures

It has 1 fixed point: (0,0,0,0,1,1,0,0)

It has 1 negated fixed point: (1,0,0,1,0,1,1,1)